Skip to main content

Understanding Complements as a Set

WELCOME Grade 9-11 Students

In today's blog we will learn about the complements as a set.

Objective:

·        At the end of this reading, students will be able to use the notation A and A' to represent the complement of sets.  

·        Use Venn diagrams to identify the complements of sets

Venn Diagrams

A Venn diagram is drawn by using a rectangle to represent the universal set and circles inside the rectangle to represent its subsets. 



 The diagram above shows a Venn Diagram and what information you are suppose to look out for or input when constructing a two (2) set diagram.

Below is a video showing how to construct a Venn diagram with 2 sets.

The Complement

The complement of a set is the set that includes all the elements of the universal set that are not present in the given set. The symbol used to identify a complement could be Ac or A'. 

Example,

If U= {pupils in my school} and X= {pupils who represent the school at games} then the complement of X is the set of all the members of U that are not members of X.  In this case, the complement of X is {pupils in my school who do not represent the school at games}.

Another example,

If U= {the whole numbers from 1 to 10 inclusive} and A= {odd numbers between 1 and 10} then the complement of A or A' is {2, 4, 6, 8, 10} which you know that these are even numbers.

The diagram below shows that the shaded region represent the complement of the given set.



Practice Questions

1.     Given the complements of Q where Q= {Thursday, Friday} if U= {days of the week} then what is Q'. 

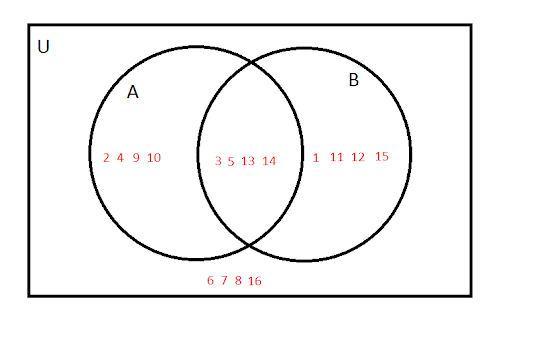
2.    From the diagram below, find

a. A'

b. B' 


Comments

Unknown said…
1. (Monday, Tuesday, Wednesday, Saturday, Sunday)
2. A’( 1,6,7,8,11,12,15,16)
3. B’( 2,4,6,7,8,9,10,16)
October 30, 2022 at 3:43 PM
Unknown said…
Q'= {Monday, Tuesday, Wednesday, Saturday, Sunday}

A'={1, 6, 7, 8, 11, 12, 15, 16}
B'={2, 4, 6, 7, 8, 9, 10, 16}
October 31, 2022 at 12:13 PM
Post a Comment

Popular posts from this blog

Difference between Union and Intersection

WELCOME Grade 9-11 Students In today’s blog we are going to look at the difference between Union and Intersection.    The union of two sets The set made by combining the elements of two sets is known as union.  It is normally represented by the symbol ∪ . The union of Sets A and B is the set of elements in A, or B or both.  The diagram below shows the universal set with set A and set B.  The shaded area is known to be the union between the two sets.   Example of Union Set If U= {11, 12, 13, 14, 15, 16, 17, 18}, A= {12, 15, 18} and B= {13, 15, 17} Then A ∪ B = {12, 13, 15,17, 18} .   Intersection of two sets The intersection of two sets has only the elements common to both sets.  This is normally represented by the symbol ∩ . The intersection of Sets A and B is the set of all elements that are common to both A and B.  The diagram below shows that the shaded region is known to be the intersection. Example of Intersection S...
1 comment
Read more

Introduction to Sets and Subsets

WELCOME Grade 9-11 students In today’s blog, we are going to look at Sets and Subsets.   Sets Sets can be seen as a collection of elements or objects, that have some characteristics in common and it is normally denoted by a capital letter.   A set may be defined by listing the members or describing them and a set can be well-defined when all its members can be listed.   A flock of sheep is an example of a defined set while even numbers less than 13 is an example of well-defined set .     Introducing Subset A subset can be defined as a part of a given set, another set or the same set.   It is normally represented by the symbol  ⊆.   If all elements of set X are in another set Y, then set X is said to be a subset of set Y.    For Example, X consist of {a, e, r} and Y consist of {a, d, e, r} therefore, X is a subset of Y because all the elements of X are present in the set Y.   The Number of Subset...
4 comments
Read more